01、二次函数的图像与性质
a的符号决定开口方向,|a|决定开口大小
① a>0抛物线开口向上;a<0抛物线开口向下.
② |a|越大,开口越大,|a|越小,开口越小
抛物线的上下平移
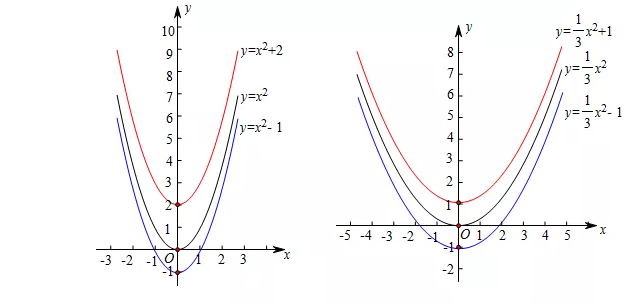
① 抛物线y=ax2+k与抛物线y=ax2,形状相同,只是位置不同.② 函数y=ax2+k的图象可由函数y=ax2的图象经向上或向下平移得到.
当k>0时,函数y=ax2+k的图象可由函数y=ax2的图象向上平移得到k个单位得到;
当k<0时,函数y=ax2+k的图象可由函数y=ax2的图象向下平移得到k个单位得到.
③ 抛物线y=ax2+k的对称轴仍是y轴(x=0).
④ 抛物线y=ax2+k的顶点坐标为(0,k).
【方法】口诀:“上加下减,上下平移在末梢”.
抛物线的左右平移
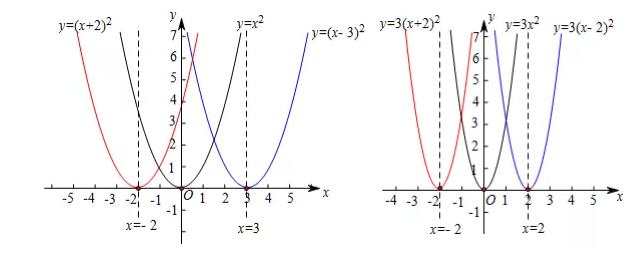
① 抛物线y=a(x-h)2与抛物线y=ax2,形状相同,只是位置不同.
② 函数y=a(x-h)2的图象可由函数y=ax2的图象经向左或向右平移得到.
当h>0时,函数y=a(x-h)2的图象可由函数y=ax2的图象向右平移得到h个单位得到;
当h<0时,函数y=a(x-h)2的图象可由函数y=ax2的图象向左平移得到|h|个单位得到.
③ 抛物线y=a(x-h)2的对称轴是x=h.
④ 抛物线y=a(x-h)2的顶点坐标为(h,0).
【方法】口诀:“左加右减,左右平移在括号”.
顶点式:y=a(x-h)2+k
当已知二次函数图象的顶点坐标(h,k)及经过另外一个条件时,设二次函数的解析式为y=a(x-h)2+k(k≠0),
再利用其他条件求出a的值,
从而求得函数解析式y=a(x-h)2+k.
一般式:y=ax2+bx+c
当已知二次函数的图象上的三点坐标(x1,y1)、(x2,y2)、(x3,y3)时,且a、b、c都为未知数时,设二次函数解析式为y=ax2+bx+c (a≠0),
再代入三点的坐标得三元一次方程组
解方程组可以唯一确定a、b、c的值,
从而求得函数解析式y=ax2+bx+c.
交点式:y=a(x-x1)(x-x2)
当已知二次函数与x轴的两个交点(x1,0) ,(x2,0)的坐标时,设二次函数的解析式为y=a(x-x1)(x-x2) (a≠0),
再利用其他条件求出a的值,
从而求得函数解析式y=a(x-x1)(x-x2),
最后将交点式y=a(x-x1)(x-x2)化简为一般式.
经过一点的圆
只要以点A以外任意一点为圆心,以这一点与点A的距离为半径就可以作出过点A的圆,这样的圆有无数个.
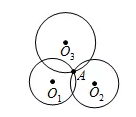
过三点的图
①同一直线上的三点不能作圆
②经过不在同一直线上的三点A、B、C,有且只有一个圆.
不在同一条直线上的三点确定一个圆.
圆心在线段AB、BC、AC的垂线平分线的交点O上,
以O为圆心,OA(或OB、OC)为半径可作出经过A、B、C三点的圆,这样的圆有且只有一个.
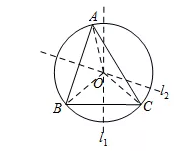
三角形外接圆
经过任意三角形三个顶点可以作出一个圆,这个圆叫做三角形的外接圆,这个三角形叫做圆的内接三角形.
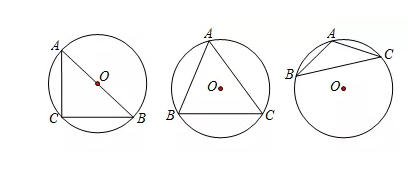
三角形外接圆的圆心叫做这个三角形的外心,是三角形三边垂直平分线的交点.
三角形的外心到三角形三个顶点的距离相等,等于外接圆的半径.
定义法
和圆只有一个公共点的直线是圆的切线.
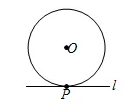
距离法
圆心到直线的距离等于圆的半径的直线是圆的切线.
当题目欲求证的直线没有明确说明经过圆上的点时,一般用此方法.方法:作垂直、证半径.
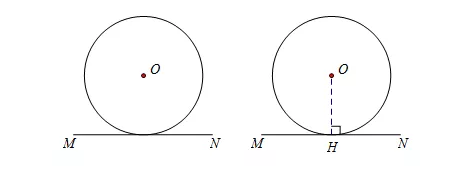
过点O作OH⊥MN于H,证明OH=r即可推出MN为⊙O的切线.
判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
当题目欲求证的直线经过圆上的点时,一般用此方法.
方法:连半径、证垂直.
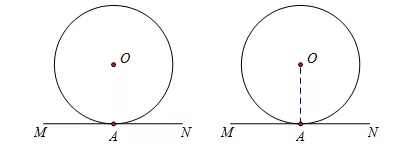
连接OA,证明OA⊥MN即可推出MN为⊙O的切线.